This project aims to provide in a didactic way the main algorithms of the graph theory in open source Octave / Matlab and Python. Please ask for any improvements (glotin@univ-tln.fr). We work on this project along the Bachelor lessons (50 hours / year) since 2007. The teachers assistants were M. Chouchane, X. Halkias, A. Mishchenko, Y. Doh, R. Bendadouche.
French Memo: ce cours donne les definitions necessaires a la théorie des graphes. Nous nous attardons au calcul des nombres cyclo et co-cyclomatiques. Une part importante du cours traite du nombre et du pôlynome chromatique. Une troisième partie pose le problème d'arbre recouvrant minimum, et la recherche du plus court chemin. Les algorithmes seront pour certains implantés, comme celui de la décomposition de Hajos pour le calcul du polynôme chromatique qui a fait l'objet de projets dirigés en 2009, et dont je donne le code ci-dessus.
PROJET de determination du nombre de colorations possibles d'un graphe avec L couleurs (polynome chromatique).
Par exemple,
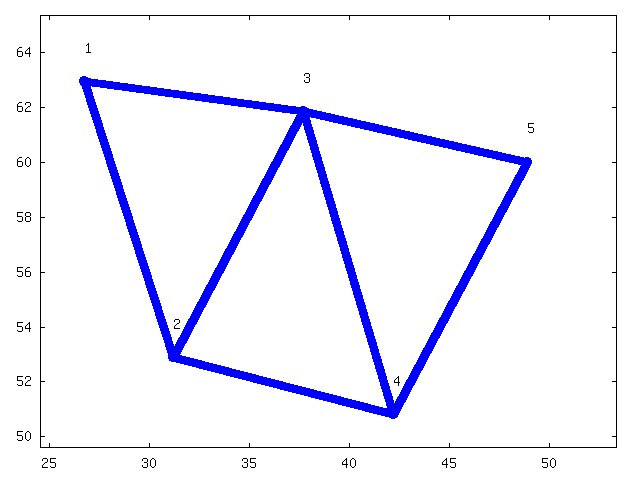
le graphe de 6 sommets ci-dessous, est coloriable avec L couleurs de n facons differentes, n donne' par ce polynome chromatique :
P(L) = [L]3 + 3*[L]4 + [L]5 ,
avec [L]N le nombre de colorations a L couleurs de la clique KN,
[L]N = L! / (L-N)! .
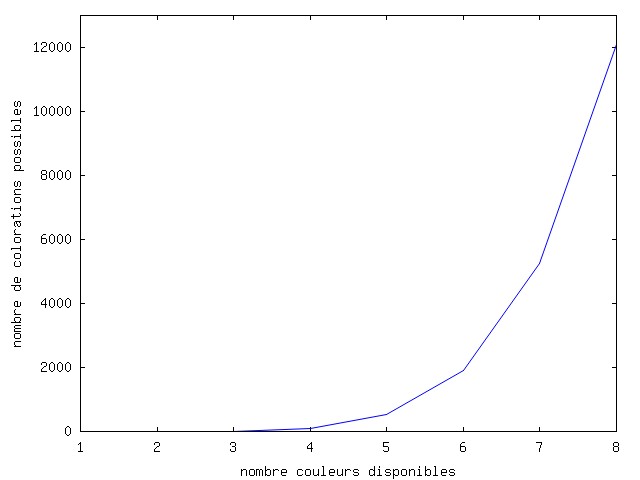
Ce graphe est donc coloriable de 6 facons avec 3 couleurs, et de 96 facons avec 4 couleurs,... Les valeurs de P pour L de 1 a 10 sont donnees dans la courbe ci-contre.


Ci-dessus nous proposons une implementation par double recursion, de l'Algorithme de Hajos, pour determiner ce polynome chromatique. Ce code (programmation vectorielle) est executable sur Octave Gnu (ou sur Matlab). Le calcul rapide, meme pour des graphes de quelque dizaines de sommets, permet en sceances de TD / TP de manipuler des graphes consequents et d'en extraire leurs parametres fondamentaux. Des heuristiques d'acceleration sont discutees en fin de module.
GRAPHE X, ordre 50, densite 1/2
GRAPHE W, ordre 3, connexe
GRAPHE Y, ordre 30, connexe
GRAPHE Z, ordre 15, connexe
GRAPHE 1, ordre 10, connexe, densite 0.5
GRAPHE 2, ordre 10, connexe, densite 0.9
GRAPHE 3, ordre 14, connexe, densite 0.9
GRAPHE 4, ordre 18, connexe, densite 0.9
gene graph
Elements de Hajos en Python
---
Polyclique :
def get_polyclique(n):
# return the polynomial of Kn
P = np.poly1d([1, 0]) # is P = L + 0 with n = 1
for i in range(1, n):
P = np.polymul(P, [1, -i]) # at step 1: L(L-1), step i: L(L-1)..(L-i)
return P
---